Duhnuts

I started writing this on 2025-05-16 then wasn’t planning to for about next year but then, Tsoding dropped this banger. I’d recommend watching that if you haven’t already, he demonstrates rotating a cube just using simple JavaScript, so comparatively it’s easier than creating a donut.
I slept at around 19:29 and woke up around 22:53, it’s around 23:31 while I’m writing this.\

You probably have seen this “🍩”, or something like this:

                                       k;double sin()
                                   ,cos();main(){float A=
                                 0,B=0,i,j,z[1760];char b[
                               1760];printf("\x1b[2J");for(;;
                            ){memset(b,32,1760);memset(z,0,7040)
                            ;for(j=0;6.28>j;j+=0.07)for(i=0;6.28
                           >i;i+=0.02){float c=sin(i),d=cos(j),e=
                           sin(A),f=sin(j),g=cos(A),h=d+2,D=1/(c*
                           h*e+f*g+5),l=cos      (i),m=cos(B),n=s\
                          in(B),t=c*h*g-f*        e;int x=40+30*D*
                          (l*h*m-t*n),y=            12+15*D*(l*h*n
                          +t*m),o=x+80*y,          N=8*((f*e-c*d*g
                           )*m-c*d*e-f*g-l        *d*n);if(22>y&&
                           y>0&&x>0&&80>x&&D>z[o]){z[o]=D;;;b[o]=
                           ".,-~:;=!*#$@"[N>0?N:0];}}/*#****!!-*/
                            printf("\x1b[H");for(k=0;1761>k;k++)
                             putchar(k%80?b[k]:10);A+=0.04;B+=
                               0.02;}}/*****####*******!!=;:~
                                 ~::==!!!**********!!!==::*-
                                   .,~~;;;========;;;:~-.
                                       ..,--------,*/

I saw this for the first time more than 2 years ago ,when I was in highschool, but I didn’t find it much interesting back then.
And then suddenly at my 4th semester, it caught my eye again. After having some idea about linear algebra, I wanted to understand the meth involved behind this. So, here’s my attempt at explaining what I’ve understood so far.

Here’s a list of things you should be familiar with:

• basic algebra
• some idea of C

Lets talk about some math

Well, how can we draw a donut?
It seems if we can draw a circle of some radius say r1 and rotate it about an axis, it’ll give us a donut(torus).
So in 3-D lets create a circle

Drawing

(r1 + r2 cos(t), r2 sin(t), 0)

this equation tells us to draw something, in the x and y axis, keeping the z-coordinate 0.

But how?

The parametric form of a circle is

x = h + r.cos(t)
y = k + r.sin(t)

Comparing with the above equation, the r1 is just and offset from the origin.

So, we get a circle at a distance of r1 from the origin and the radius of the circle generated itself is r2.

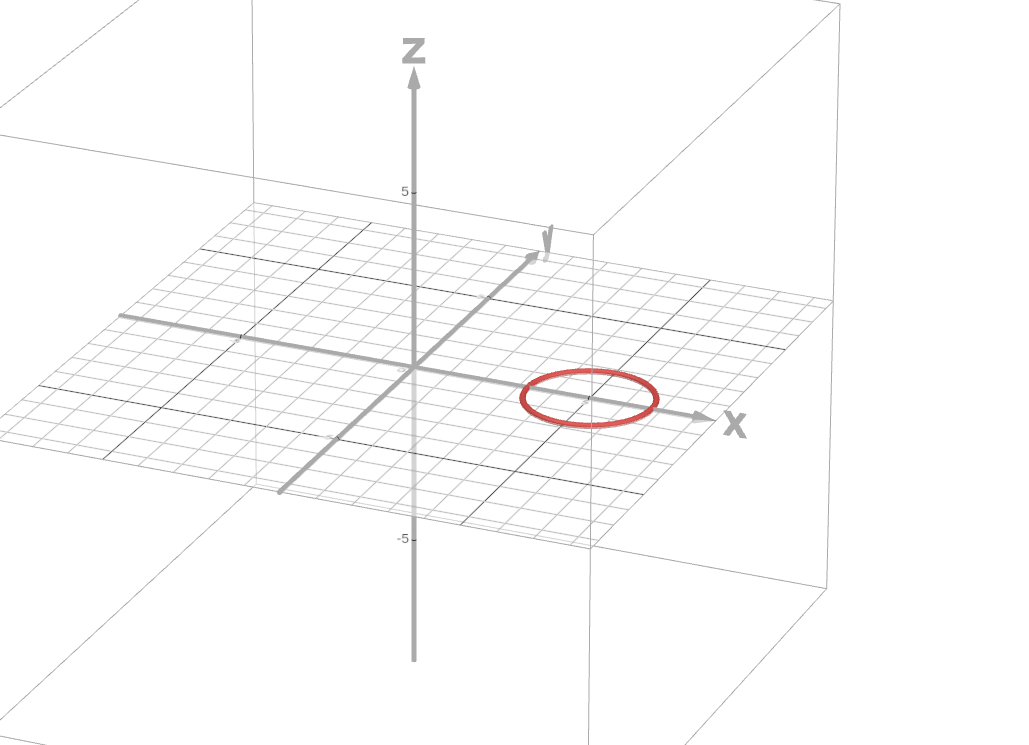
Creating a torus

So if we rotate this circle about an axis, we should get a torus.
Check this out:

To be continued…